Why don't large models overfit?
An exploration of the double descent phenomenon
Summary by Adrian Wilkins-Caruana
A well-known rule in statistical machine learning is that a statistical model shouldn’t have more parameters than the number of samples that were used to train it. That’s because the model will have enough parameters to fit each of the samples exactly, and so it will be less likely to generalize to unseen data. But this rule is seemingly contradicted by modern deep neural networks like Llama 3 and Stable Diffusion — models that have hundreds of billions or even trillions of parameters. Why can models like these generalize well to unseen data even when their training data size is smaller than their parameter counts? This week’s Learn & Burn will cover this strange phenomenon, known as double descent, rather than our typical focus on a single research paper.
Double descent is a phenomenon where a model can continue to generalize well to unseen data even when it has many more parameters than training data samples. The figure below demonstrates this using a polynomial fitting example. The main thing being compared is the parameter count, or degree, of the polynomial, and whether it is less than, approximately equal to, or greater than the number of training samples.
Let’s look at these cases one by one:
On the left, the degree-1 polynomial doesn’t fit the data well because it doesn’t have enough parameters to fit the nonlinear training data.
In the middle, it looks like the fitting problem is solved, since the degree-10 polynomial fits the 11 data points precisely. But a precise fit isn’t ideal since any unseen data drawn from the same distribution as the training data probably won’t fit exactly on this polynomial’s curve. This problem is called overfitting.
Finally, on the right, the degree-30 polynomial seems to fit the data quite well, despite having substantially more parameters than the training data that it’s being fit to.
We need to include some regularization in the final curve’s optimization; otherwise it would look “bumpier” in order to fit exactly through every point. As we’ll see below, researchers suspect that models that learn in a regularized fashion (intuitively, they prefer learning simpler patterns) correlate with the double descent phenomenon.
(Side note: About a year ago, Yann LeCunn, the Chief AI Scientist at Meta, gave a brief explanation of the double descent phenomenon in this fireside chat. He said that the double descent phenomenon can be observed with polynomial fitting, too. A curious viewer then asked Claude, an LLM like ChatGPT, to write some code that demonstrates double descent with polynomial fitting. The figure you saw above is the one that Claude’s code generated!)
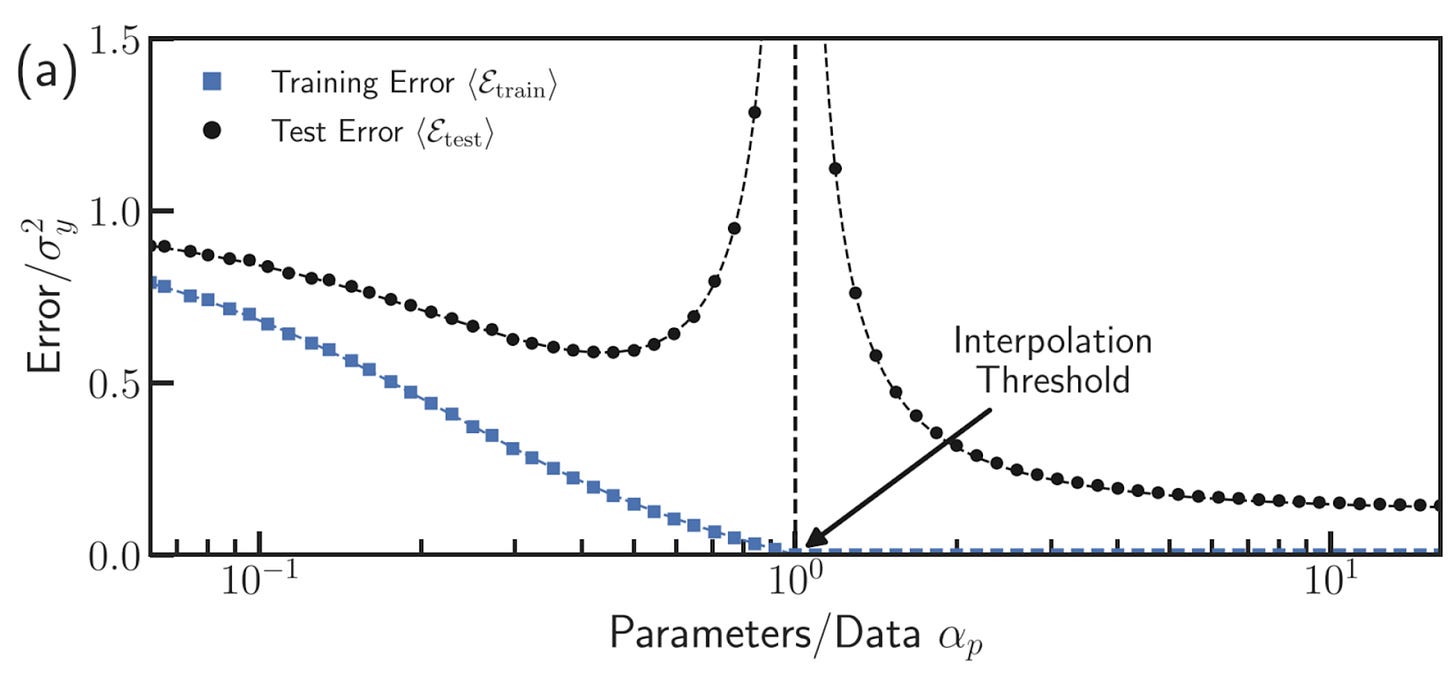
Here’s another figure (from Wikipedia) that I really like that helps explain double descent. Like the sequence of plots above, from left to right, the x-axis shows the behavior of a two-layer neural network when the number of parameters is less than, equal to, and greater than the number of data points. But this time the y-axis shows the training and test errors. We can see where the double descent phenomenon gets its name: As the number of parameters increases, the test error descends, before increasing at the interpolation threshold, and then continuing to decrease again.
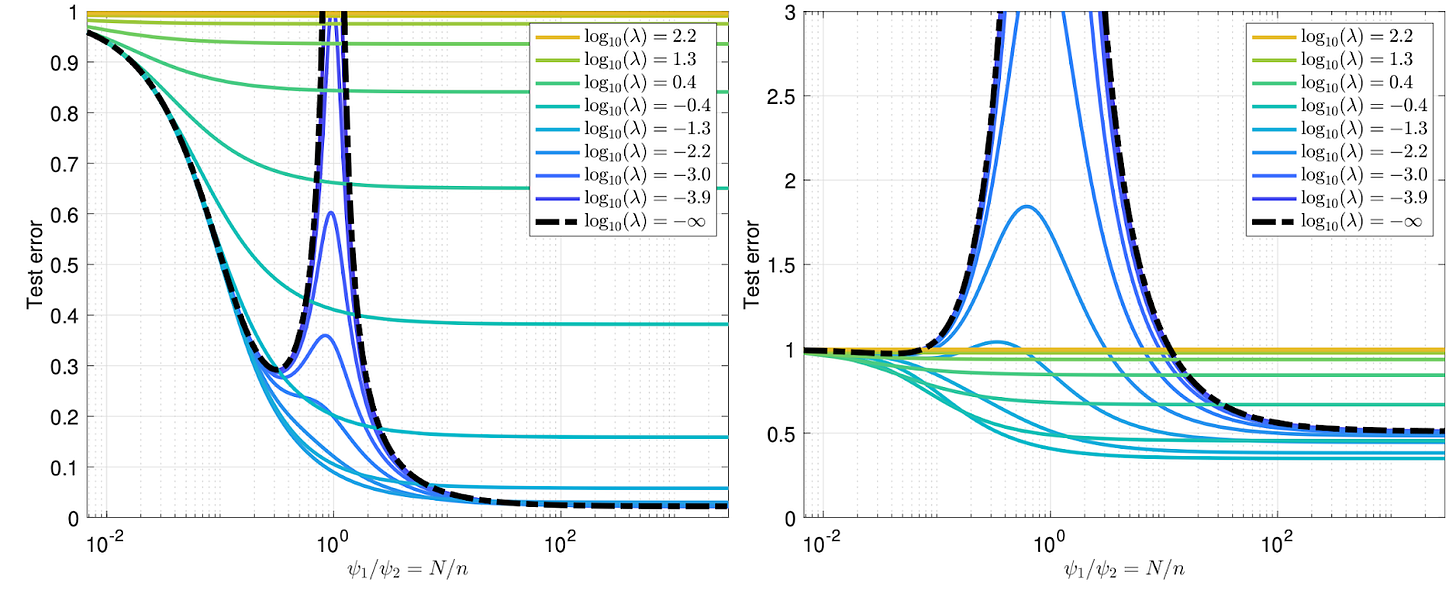
Why do neural networks behave this way? We still don’t know the precise answer, but researchers have established that the data’s signal-to-noise ratio (SNR) and the amount of regularization used during training are central to the phenomenon. The figure below shows how these characteristics influence double descent. The show results on datasets with high (left) and low (right) SNR, and the colors show results of models trained with different levels of regularization (low regularization = blue, high regularization = yellow). We can see that, without regularization, the double descent phenomenon occurs regardless of the SNR. But when regularization is used, its optimal value — indicated by a test error that doesn’t increase at the interpolation threshold N/n=1 — is slightly different in the high- and low- SNR cases.
Image source: Fig 3 of https://arxiv.org/pdf/1908.05355
Double descent and related strange phenomena that arise when we train neural networks — like grokking — still aren’t entirely understood. Researchers are still trying to develop solid theoretical explanations for why they happen. So far, we understand small pieces of the double-descent puzzle, such as:
Poor generalization is most likely at the interpolation threshold
Models with optimal test error typically lie beyond the interpolation threshold
The behavior of double descent depends on the SNR in the data and regularization (like in the figure above)
If we’re lucky, the next time I talk about double descent on Learn & Burn will be when someone properly cracks the double-descent problem wide open!