LLMs only need three weight values (-1, 0, and 1)
[Paper: The Era of 1-bit LLMs: All Large Language Models are in 1.58 Bits]
Summary by Adrian Wilkins-Caruana
Years ago when I graduated from university, my first job was to design parts of logic chips that implement data-compression algorithms. This meant that I needed to understand the compression algorithms themselves and needed to modify them so that I could minimize the number of logic gates they used. (If you’re familiar with FPGAs, I was trying to minimize lookup table usage.)
One of these compression algorithms was based on a small neural network (NN). Using what was cutting-edge research at the time, I figured out how to replace the NN’s floating-point arithmetic with fixed-point, integer-based arithmetic. This was a boon for minimizing logic usage, since integer-based arithmetic is far simpler to implement than floating-point arithmetic. While I was quite impressed with my achievements at the time, these kinds of NN optimizations have come a long way since then. Today’s paper presents one such example: BitNet b1.58. (I’ll explain where this magic number 1.58 comes from below.)
BitNet b1.58 is a peculiar NN proposed by GeneralAI, a Microsoft-backed research lab based in Beijing. It builds upon an LLM called BitNet, which is previous work from the same lab that aims to make NN-computations more efficient by reducing the number of bits used in each operation. The bit-reduction techniques fall on a spectrum:
On one end, vanilla NNs typically use 32-bit floating-point (or fp32) values, which is the standard data format for doing math with real numbers.
With some loss in precision, fp16 can be used instead of fp32, which yields some computation and memory benefits.
Fixed-point based methods typically use 8-bit integers (int8). This approach can often be substantially more efficient than fp16 (especially for hardware optimized for integer arithmetic), but with substantial added complexity and loss in precision.
Finally, BitNet takes bit-reduction to the extreme. It uses 1-bit weights — that is, the weights are either +1 or –1.
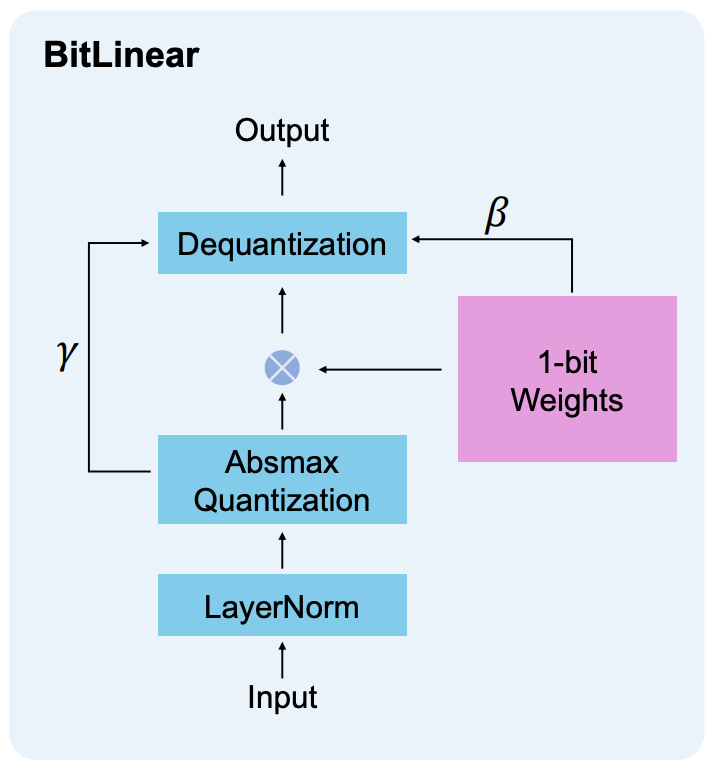
Before I describe BitNet b1.58, it’s worth understanding BitNet a bit more. A NN with 1-bit weights involves completely re-thinking how a NN functions, down to the individual math operations it uses. For starters, BitNet only uses 1-bit operations for the fully-connected layers in its transformer architecture, though these layers account for the vast majority of the LLM’s computational requirements. BitNet’s replacement unit for a fully connected component is called a BitLinear module. The BitLinear’s activations and intermediate results are stored in higher, 8-bit precision. The image below shows the layer, with β and γ being additional values that BitLinear uses to dequantize the accumulated result (which I’ll discuss next) into the 8-bit range.
NNs are mostly comprised of matrix-multiplication operations, which can be implemented using several multiply-accumulate steps: Multiply a weight and an input value, accumulate the result, and repeat. The genius behind using weights that are either +1 or –1 is that the multiplication step can be simplified to an addition (or subtraction) instead: Given the value of the weight, add (or subtract) the input from the accumulator.
This is where BitNet b1.58 comes in. The “b1.58” part of its name is derived from how many values the weights can take: Instead of just +1 and –1, BitNet b1.58 adds in a third value, 0. So, instead of it using 1-bit weights like BitNet, it uses log2(3) = 1.58-bit weights. (The math works like this: If we could have ~1.58 bits, then those bits could store ~2^1.58 different values — that is, ~3 values.) Also, BitNet’s accumulate-only property is retained: Instead of adding (or subtracting) only, now there’s a third option, “do nothing with this input.” One downside of the BitNet approach is that the LLM must be trained from scratch: An existing model can’t just be converted to a 1-bit or 1.58-bit NN. However, fp32 models can be converted to fp16 or even int8 without full retraining.
By this point, you might be asking yourself, “If BitNet was so good, how can adding an additional weight value be beneficial for computational efficiency?” To answer this question, I would really love to show you some experimental results comparing BitNet to BitNet b1.58, but unfortunately the paper doesn’t include such a comparison. But I think we can intuit the following:
The size of the weights in memory will at least double since two bits are required to store a ternary without compression (i.e., you can’t actually have 1.58 bits).
The additional algorithmic complexity induced by the 0 weight should have negligible effect on runtime compared to the original BitNet.
The language-modeling accuracy should improve compared to BitNet, since the weights can be more precise.
The results shown in the paper compare BitNet b1.58 to Llama (the original, not Llama 2). Across seven different tasks and three different model sizes (700M, 1.3B, and 3B), BitNet b1.58 performs within ~1% of Llama. Also, the figure below shows the latency and memory required for Llama and BitNet b1.58, and highlights how much more efficient the new approach is on an equal-parameter basis. Interestingly, the authors also report efficiency improvements for 13B- and 70B-sized models, but they don’t discuss the comparative accuracy of these model variants.
The final, and perhaps most important part of optimized NNs is the hardware that they run on. The creators of BitNet b1.58 made their comparisons using GPUs, so I think we can assume that BitNet models run more efficiently on GPUs than on CPUs. I’d say this provides a fair comparison, since specialized hardware for running 1-bit NNs doesn’t exist yet. But the authors note that hardware specifically designed for 1-bit NNs would yield significantly better performance.
Ultimately, the way we run NNs is up to chip designers. Anecdotally, I’d say there has been a convergence on fp16 (and related 16-bit floating point formats) for NN computations, especially in GPUs and Google’s TPUs. But, regardless of whether these hypothetical efficiency gains are realized with specialized hardware, the BitNet b1.58 approach could be a very effective way to run LLMs on consumer devices that don’t have a lot of computing power, like phones and smartwatches.