How to tell if an LLM is just guessing
[Paper: Detecting hallucinations in large language models using semantic entropy]
Summary by Adrian Wilkins-Caruana
LLMs like GPT-4 and Gemini act like they know everything. They do know a lot of stuff, but certainly not everything. LLMs also speak confidently, rarely saying things like “I don’t know the answer to your question” or “I’m not sure.” This leads to a widely known problem: LLMs sometimes hallucinate or confabulate information to fill in gaps in their knowledge. This is frustrating and it severely limits their ability to be used in real-world situations, since it’s really hard to fact-check everything an LLM says to make sure it isn’t just making stuff up. But a new paper published in Nature proposes a statistical way to detect hallucinations.
The main piece of information that makes confabulation-checking possible is that, when an LLM generates some text, it also says how confident it is about each token that it generates given the tokens that came before. Using these confidence probabilities, there’s actually a simple approach to detecting hallucinations. For example, we could use the following process to detect whether an LLM’s answer to the question “Where is the Eiffel Tower?” is a hallucination:
Ask the LLM to generate many different answers to this question.
Aggregate the probabilities from the tokens within each answer individually.
Combine the probabilities over each answer into a single value, called predictive entropy, which is the conditional entropy of possible answers to the question.
When the predictive entropy is low, it means that the distribution of answers is heavily concentrated to a small number of answers. When it’s high, it means many answers are equally likely.
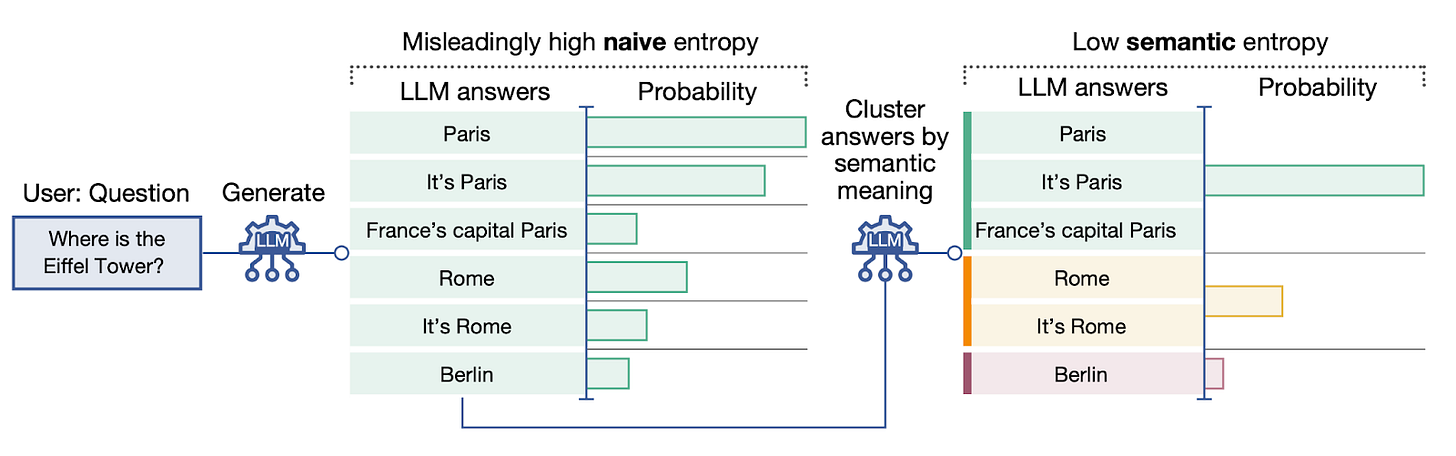
But there’s a big problem with this approach, as you can see in the figure below. There are many different ways an LLM can answer a question, and sometimes the aggregated probabilities of correct answers are lower than those of incorrect answers. For example, the example shown below indicates that “France’s capital Paris” has lower probability than the hallucination “Rome.” This can result in a misleadingly high naive predictive entropy, even when the space of possible answers is in fact skewed to a small number of answers that, in this example, are not hallucinations.
You can probably see the issue with naive entropy in this example: Even though the answer “France’s capital Paris” is correct, it’s just not the way one would typically answer the question. The authors’ solution to this problem is to calculate the entropy across the semantic categories of the LLM’s responses rather than the responses themselves. Semantic equivalence is a relation that holds when two sentences mean the same thing — this idea can be extended to group any number of outputs from the model into these categories. There are two things we need in order to do this: First, a way to find these semantic categories and know which sequence belongs to which category, and second, a new way to combine the sequence-probability values into a final semantic entropy.
To solve the first problem (grouping together similar answers), the authors use special LLMs that determine whether two sentences are semantically equivalent (i.e., mean the same thing). These LLMs can be specialized for this task, such as DeBERTa-Large-MNLI, or general-purpose LLMs like GPT-3.5 that can predict when one bit of text implies another, given suitable prompts.
Once this model has determined which answers belong to the same semantic group, their sequence probabilities need to be combined. Mathematically, this involves summing all the sequences of a given group together. Then, the probabilities of all the semantic groups are combined into a value that the authors call semantic entropy, which is similar to how individual sequence probabilities are combined in naive entropy. The authors also have another way to calculate semantic entropy when they can’t access the sequence probabilities: They assume each sequence has equal probability, and thus each semantic cluster’s probability is proportional to how many sequences were generated in that cluster. They call this value discrete semantic entropy. This approach makes sense if you have many sample points because you expect to see repeats of answers in proportion to how likely they are. (But, if all the probabilities are very small, then you only ever see each answer once, and the regular semantic entropy value is clearly more accurate.)
To use the semantic entropy approach, an LLM generates many answers to a question, and the authors choose an answer from the highest-probability semantic cluster as the final answer. The figure below compares their two methods: semantic entropy (blue) against naive entropy (green) and other baselines (red and yellow) on QA and math tasks. The AUROC metric captures how well the model can distinguish between hallucinations and non-hallucinations, where a value of 0.5 indicates the result from random chance. The AURAC metric, which the authors invented, tracks (but isn’t identical to) the accuracy of answers given by a model which can say “I don’t know” when it notices itself hallucinating. In other words, the AUROC score measures how good a system is at noticing hallucinations, and the AURAC score measures how good the system is after filtering out hallucinations. In both cases, higher is better, and the two scores may be quite different because the AURAC score depends heavily on the accuracy of the underlying model, such as LLaMA 2 or Falcon.
Overall, I think the semantic entropy approach is fantastic. It uses information and models that are already available (token probabilities and semantic equivalence models) and clever statistical tricks to detect confabulations, without having to train specialized models like the baselines do. In fact, this points to something a bit deeper: The red-colored baseline in the figure above is from a paper titled “Language Models (Mostly) Know What They Know.” The title indicates that LLMs actually have some awareness of when they’re making stuff up. The result from this paper adds more weight to that idea. To me, this suggests that hallucinations and confabulations are a consequence of the way we’re training LLMs. Maybe we just need to find a way to train LLMs to know when to say, “Sorry, I don’t know.”