Dramatically more efficient LLMs via fast feedforward networks
Paper: Exponentially Faster Language Modeling
Summary by Adrian Wilkins-Caruana and Tyler Neylon
Have you noticed that many AI-based features on your phone or computer require an active internet connection to function? That’s because the neural networks that support these features are computational behemoths — they run on specialized hardware in data centers rather than on your device. But why can’t these models, like LLMs, run on your device? The answer isn’t simply “bigger models need bigger computers.” In fact, the topic of today’s summary is about a new way to design neural networks that could, in theory, allow LLMs to run on your phone without it even breaking a sweat. But, as we’ll see, the reality is more nuanced than the theory would suggest.
Researchers from ETH Zürich recently introduced a variation of the feedforward network (FF) called a fast feedforward network (FFF). We’ll discuss how each of these networks works in a moment, but the gist of their contribution is that an FFF network is much faster than an FF network — up to 220x faster. Since FFs are a quintessential component of many neural networks, FFFs could enable efficient processing of big models like LLMs on your phone or laptop. But before we can understand why it’s not that simple, we need to understand the differences between FFs and FFFs.
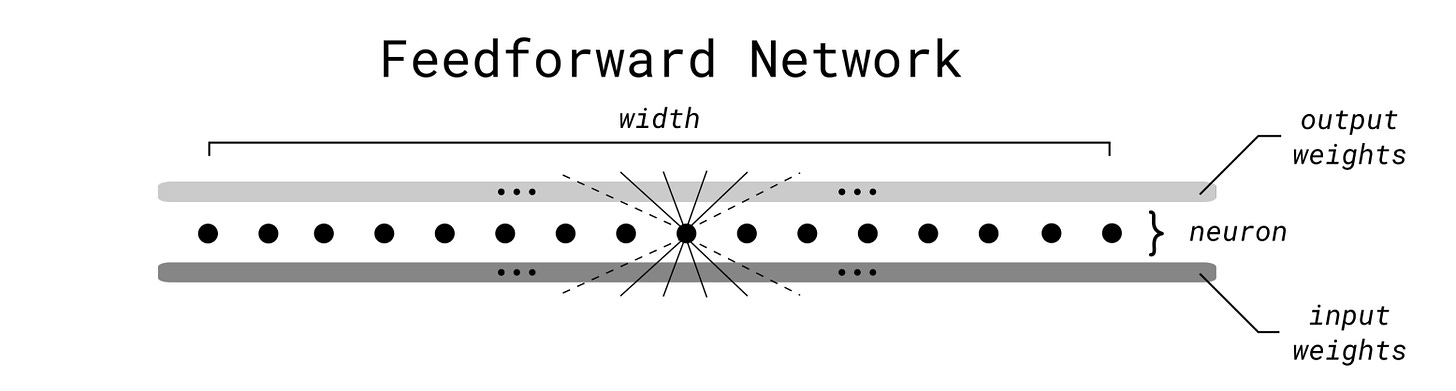
An FF network is a very simple neural network. While a general FF network may have multiple hidden layers, these authors focus on FF networks with exactly one hidden layer (you can simulate more hidden layers by stacking several of this “simple” kind of FF). So, for these authors, an FF network has one input vector, one hidden layer, and one output layer. Mathematically, if the input vector is x, then we could model such a layer like this, where M and N are matrices:
Using the words “input,” “hidden,” and “output” as variables for the respective lengths of those vectors, matrix N would have size hidden × input (thus converting an input-length vector into a hidden-length vector). And matrix M would have size output × hidden, thus converting the hidden vector (the output of σ(N⋅x)) into an output-sized vector.
In the illustration below, the matrices M and N are represented by the two horizontal lines of weights. The values in matrix N are the “input weights” since this matrix operates on the inputs, and M’s values are the “output weights” since this matrix provides the (pre-activation-function) output vector.
The simplicity of FFs comes at the cost of a lot of unnecessary computation, since, as neurons become more specialized for specific kinds of inputs, they often won’t add much information for inputs outside of their specialties. FFFs are an attempt to reduce this unnecessary computation.
An FFF acts like a binary decision tree where the leaf nodes are small FFs and non-leaf nodes are tiny neural networks. During inference, each decision node provides a single value y = σ(N⋅x), where x is the input vector to the FFF. If this value y is < ½, then the left child of the decision tree is consulted next; otherwise the right child is used. Once a leaf node is reached, a standard FF network is applied to the input x. This leaf node is much faster than a regular FF because its output is smaller. The reason a smaller output (from the leaf node) can provide the same value as a larger-output FF is that more knowledge has gone into choosing the correct leaf. The authors draw an analogy between leaf-choosing and expert-choosing in a mixture-of-experts model.
But since decision trees aren’t differentiable, you might ask: How can we train such a conditional beast? Brilliant question, reader. The authors address this by using a slight variant of the model that is differentiable during training, and slowly moving this model toward the final, non-differentiable behavior as training concludes. During training, every node of every decision tree is computed. Instead of providing only the output of a single leaf, all leaf values are computed, and the final FFF value (again, only during training, not inference) is a weighted combination of all these leaf values. The weights are the strength of each respective path to that leaf. This way, the final FFF value depends on all of its weights, and the FFF, as a mathematical function, remains everywhere differentiable, so that its weights can be learned.
Here’s the main point: At inference time, only a single path and a single leaf node of an FFF is ever computed. If the depth of the tree is d, this involves only computing d non-leaf nodes and a single leaf node, and the intuitive “learning value” of that final output is based on training O(2^d) weights. In a sense, it’s an exponential efficiency gain in number-of-weights-trained versus number-of-weights-used at inference time. The illustration below outlines the FFF architecture.
To test the modeling accuracy of FFs vs. FFFs, the authors modified a standard BERT model to make UltraFastBERT, an LLM built with FFFs instead of FFs. Their results showed that UltraFastBERT retained at least 96% of the performance of BERT-base, a model with the same architecture, but built with FFs instead of FFFs. It’s fair to say that the output of an FFF-BERT model is about as good as a normal BERT model. Yet, when it comes to inference speed, UltraFastBERT can perform up to 255x faster than BERT-base when running on a CPU, and up to 118x faster when running on a GPU (with a theoretical limit of being 341x faster).
That sounds too good to be true, right? If an FFF LLM is two orders of magnitude faster than an FF LLM, why don’t we use FFFs all the time? The answer lies in the hardware that runs them. Even though UltraFastBERT was 255x faster than BERT-base on a CPU, this isn’t a practical demonstration of how to run a neural network, since GPUs are more suitable for this task than CPUs. An FF LLM running on a GPU will still be a lot faster than an FFF LLM running on a CPU because GPUs are efficient at standard FF computations and relatively slow at handling conditional branching. Even though the authors say UltraFastBERT is 118x faster on GPU, this isn’t practical either: Their results demonstrate apples-to-apples comparisons of naive FFF and FF software that doesn’t really reflect the code that’s actually used to process neural networks. In other words, typical production-ready FF code is highly optimized in its own way.
What does all this mean for FFFs? Unfortunately, even though FFFs are in theory much more efficient than FFs, in practice it boils down to how fast a computer chip can process each neural network. To use an FF, a computer processor performs something called a dense matrix multiplication (DMM). DMMs are so common in computing that we have special, super-optimized hardware for executing it. On the other hand, an FFF uses a conditional matrix multiplication (CMM), and we don’t have hardware that’s good enough to run an FFF faster than an FF using DMM. Ultimately, it’s up to chip designers — and the algorithms they choose to optimize their chips for — to determine whether we’ll one day see FFF-based neural networks.