Do LLMs rely on data contamination to solve math problems?
[Paper: GSM-Symbolic: Understanding the Limitations of Mathematical Reasoning in Large Language Models]
Summary by Oreolorun Olu-Ipinlaye
Computers have always been great at math — or at least at mathematical operations. You plug in numbers and math operands and you get a result. But computers couldn’t solve word problems until LLMs arrived. That’s because solving word problems requires natural language processing (NLP) and logical reasoning. But how well do LLMs actually handle math problems? Do they logically reason through them or do they just rely on the knowledge of similar questions that they were trained on? That’s the subject of today’s paper.
LLMs have been quite impressive when evaluated on the Grade School Math 8K (GSM8K) dataset, a popular dataset for evaluating LLMs on multi-stage mathematical reasoning tasks. But the authors of today’s paper argue that GSM8K isn't sufficient for accessing mathematical reasoning, so they created a new dataset, GSM-Symbolic which is derived from GSM8K but lets researchers generate different versions of the same question.
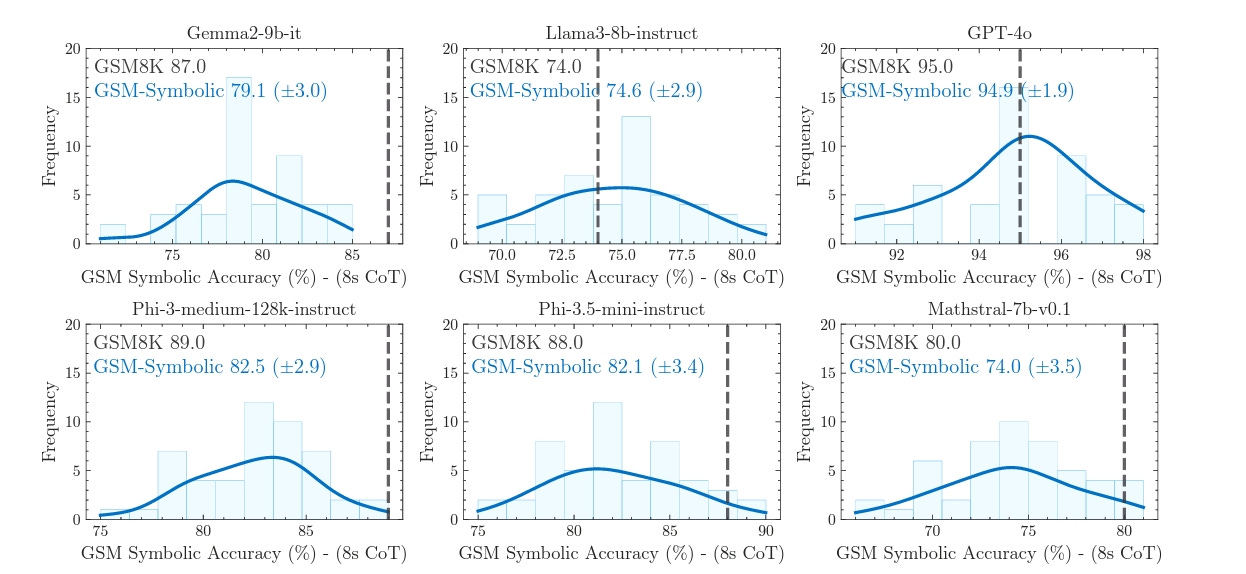
As you can see in the image below, GSM-Symbolic is a template that allows for question variables to be swapped out. The researchers did this because they wanted to investigate how an LLM’s accuracy changes when one or more variables are changed. They generated 50 different variations of 100 questions in the original GSM8K dataset, for a total of 5,000 questions. They then evaluated over 20 models, both open and closed source, and I must say the results were quite surprising.
They discovered that by simply changing the variables of a math problem, model accuracy across most LLMs varied significantly, so much so that they actually termed it a distribution — little wonder why when you see the image below. Not just that, but average model performance was also lower compared to evaluations done on the GSM8K dataset.
The researchers also discovered that the models were more sensitive to changes in numerical variables than to changes in names; performance dropped significantly more when numbers were changed. So why are the models so sensitive to changes in variables? The authors make a very valid argument as to why: data contamination. They argue that since the GSM8K dataset is so popular, there’s a chance that some of its questions have been used to train LLMs and the models have simply memorized these questions or learned to associate logical patterns with them.
But wait, there's more! The authors also investigated how question difficulty affects performance. They made questions simpler by removing clauses and harder by adding more, and discovered that performance drops and variance increases as question difficulty increases. Finally, they designed experiments to test whether the models actually understand mathematical concepts. They did this by sneaking in random clauses that have no relevance to the math logic required in solving the questions. As you can likely guess, model performance dropped significantly across all models, indicating that they picked up on the irrelevant clauses and attempted to use them in solving problems.
What does this all mean? We’ve all experienced token bias when using LLMs: You structure your prompt slightly differently and you get a different response. In a logical process like math, though, the expectation is that the model must have learned the underlying logic of solving similar problems — but apparently not. The fact that changing numerical values, the very essence of math problems, was a factor in accuracy is a clear indication that the models haven’t learned and don’t follow the required logical reasoning steps for solving word problems. Could it be just because of data contamination? Clearly more investigation is needed. Personally, I’d love to see how the models perform on more complex word problems since GSM-Symbolic is a grade-school level dataset.



This warms my heart !