AI is solving international-level math competition problems
[Article: AI achieves silver-medal standard solving International Mathematical Olympiad problems]
Summary by Adrian Wilkins-Caruana
[The original DeepMind article]
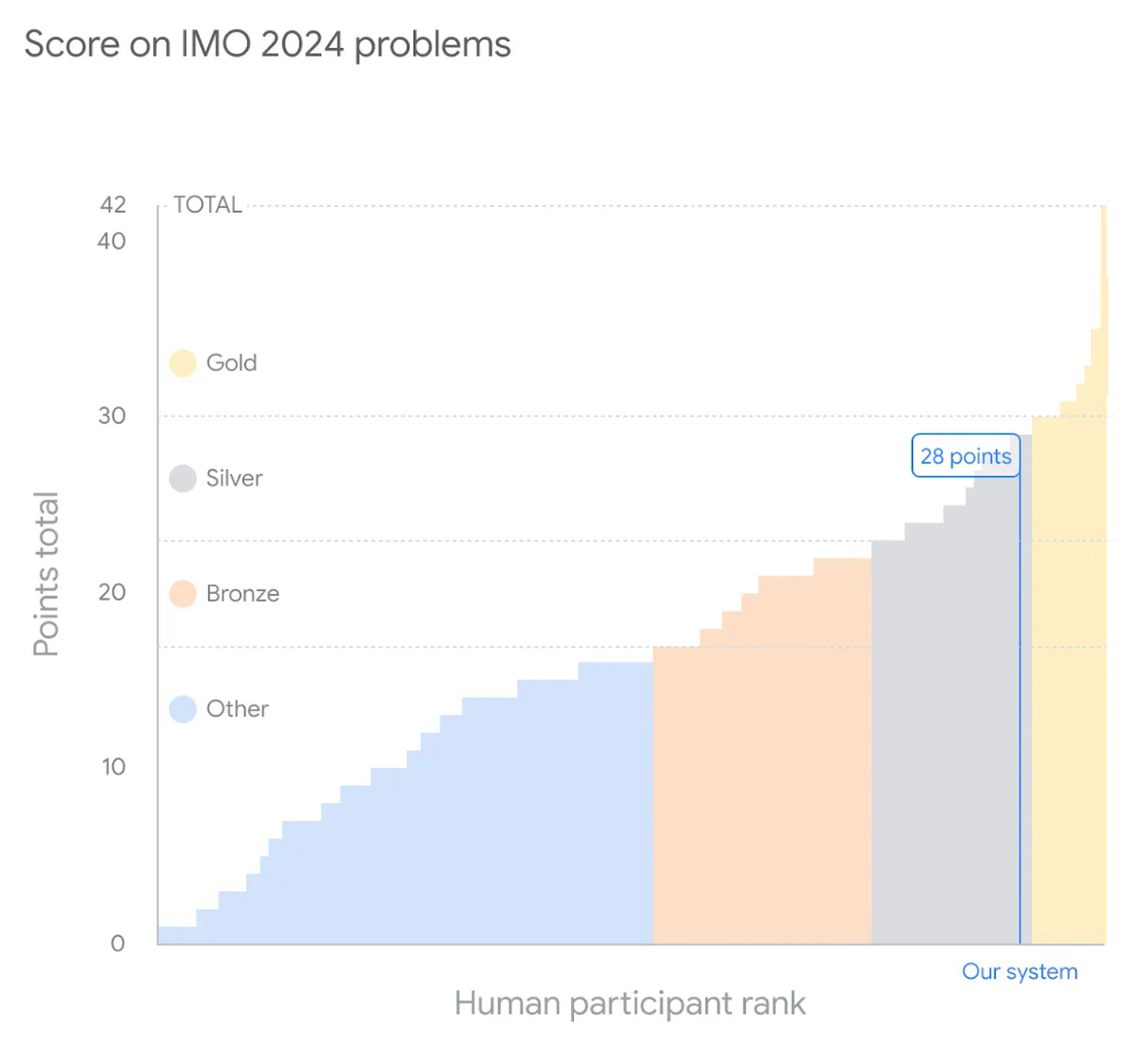
The International Math Olympiad (IMO) is an annual competition where rising stars in mathematics represent their country in a test of their abilities. One of the contestants in this year’s IMO was a peculiar stateless entrant, backed by the folks at Google DeepMind. The entry consisted of the joint efforts of two AI systems: AlphaProof and AlphaGeometry 2. The system scored a total of 28 out of 42 points, or, put another way, it got perfect scores on the four (out of six) problems it managed to solve, and none for the others. It placed 58th out of 609 contestants, which this year equated to a silver medal.
First, some groundwork: Regular human contestants have just two 4.5-hour blocks to submit solutions, but Google DeepMind’s systems took longer than that. AlphaGeometry 2 solved one problem within minutes, but AlphaProof took three days to solve two algebra problems and one number theory problem. The systems weren’t able to solve the other two problems, which covered combinatorics. So, this AI participant wasn’t really a contestant, but I don’t think that takes away from Google DeepMind’s achievement.
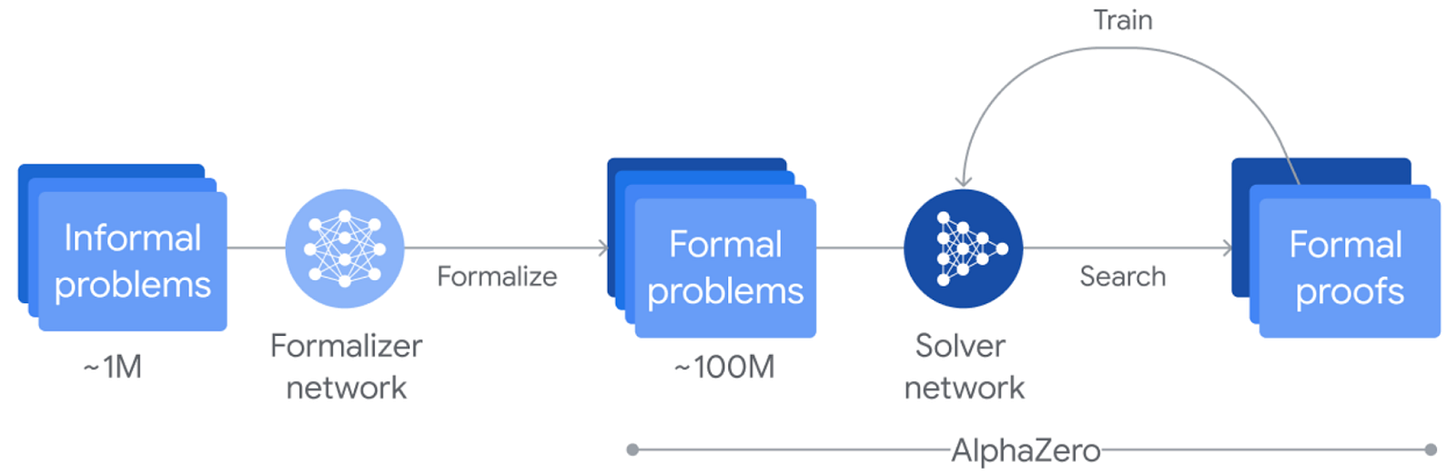
As its name suggests, AlphaProof proves mathematical statements, and it does this using a combination of two things. The first is a software tool called Lean, which verifies whether a proof of a mathematical statement is correct. Proving something in Lean is kind of like finding a path from your house to the grocery store. The proof itself is a series of moves or proof steps, like “turn left” and “stay on Biscayne.” Lean checks each step to make sure it's valid, which is important because, depending on the state of the problem, not all moves are valid. The second part of AlphaProof is AlphaZero, which is the same path-finding AI that Google DeepMind previously used to master chess, shogi, and Go, and it works in much the same way as AlphaProof: by evaluating which paths show promise.
But doing mathematical proofs is quite different from playing chess or Go. The researchers needed to train the system on the types of problems that AlphaProof would encounter in the IMO. So they fine-tuned a Gemini LLM to translate natural language problem statements into formal ones. Then, using a dataset of ~100k formal problem statements, the researchers trained AlphaProof to prove or disprove them by searching over possible proof steps (i.e., moves) using Lean. When Lean says that the series of steps satisfies the original problem statement, it’s done! Each proof that AlphaProof finds reinforces it, enhancing its ability to solve problems. The figure below shows this process.
AlphaGeometry 2 takes a slightly different approach. The Google DeepMind researchers describe it as a “neuro-symbolic” hybrid system since it uses a language model (based on Gemini) and a symbolic engine. This approach starts by representing the geometric problem as a graph (or network) of geometric symbols (e.g., a point, line, angle, circle, segment, etc.). Then, a language model suggests some next steps (e.g., construct D: midpoint BC). Next, using some primitive geometric relationships like the behavior of parallel lines or midpoints, the symbolic engine searches over possible next steps (kind of like AlphaZero) to see if it can reach the goal of the proof. For instance, in the example below, the language model suggests a construction that helps prove that the triangle is isosceles where, in the right frame, the first blue statement represents the construction, and the subsequent ones represent the subsequent symbolic deductions.
TWIST! What I described just above was actually AlphaGeometry (the original, which was announced in January 2024), not its successor. AlphaGeometry 2 includes three main enhancements that help it solve much more challenging problems:
It’s trained on an order of magnitude more synthetic data.
Its symbolic engine is two orders of magnitude faster, allowing it to expand its search for solutions.
It uses a novel knowledge sharing mechanism, which lets the deduction engine share information from disparate steps/constructions and their subsequent deductions, and — if helpful — combine these disparate steps.
When I was studying math in school, I often found myself using WolframAlpha to check my answers or my work. I see Google DeepMind’s system as an extension of this idea, where mathematicians can use tools like this to help them solve and verify solutions to problems. To some extent, this is already happening!
This year, Australian mathematician Terrence Tao presented a talk on “machine assisted proofs,” where he said that he suspects it’s ~20x harder to write formal proofs (ones computers can verify) than informal ones (ones that mathematicians write, publish, and peer-review). However, he also said that AI integration could change this, potentially tipping the balance in favor of formal proofs, which would have a dramatic impact on the field of mathematics. If we extrapolate the rate of progress made by AlphaGeometry over this year alone, it seems that the balance is definitely shifting, and potentially quite rapidly.