A new weakness in LLMs: early vs late token importance
[Paper: Transformers need glasses! | Information over-squashing in language tasks]
Summary by Adrian Wilkins-Caruana
Black holes are extreme objects that demonstrate some of the complex and bizarre ways that the universe works. For example, imagine you were observing an orbiting planet transit across the far side of a black hole. At the moment that you, the black hole, and the planet were in perfect alignment, the planet would look to you like a squished ring around the black hole. This is because of a strange phenomenon called gravitational lensing that happens since the black hole’s gravitational field distorts spacetime; i.e., light no longer travels in a straight line! This distortion can be quite counterintuitive because the mental model of spacetime that we use on a daily basis (that light travels in straight lines) is a simplification of the more complicated reality that’s better described by Einstein’s general relativity.
As someone who thinks about machine learning frequently, I find that my brain also constructs similarly helpful-yet-simplified models of machine learning-related concepts, like transformers. For example, when I see the phrase “transformers are next-token predictors,” my brain often reads this as “transformers predict the next word in a sentence, kind of like how a person might anticipate a sentence’s continuation.” Unsurprisingly, mental models like these, while helpful, are imprecise. But what is perhaps a surprise is that, mathematically, this particular mental model is imprecise in a very similar way to how our mental model of the spacetime doesn’t reflect the reality described by general relativity. 🤯
Researchers from Google DeepMind have investigated how information propagates in decoder-only transformers. They found that transformers definitely don’t continue sentences the way that a person might because of a subtle detail relating to how transformers work that my simplified mental model (the finish-a-sentence model) doesn’t capture.
Here’s a simple illustration of the researchers’ experiments. Imagine asking a transformer what it “thinks” after showing it a sequence of digits. The sequence contains only ones, except for the last digit, which is zero. Here’s what they found: As the number of ones increases, the transformer’s last-token representation (i.e., what it “thinks”) converges. In other words, the representations of the strings 10 and 110 are very different, but the representations of strings with 1,000 ones and 1,001 ones are basically the same. The figure below shows this phenomenon, where the color and proximity of the curved lines illustrate how these representations converge as the sequence length increases.
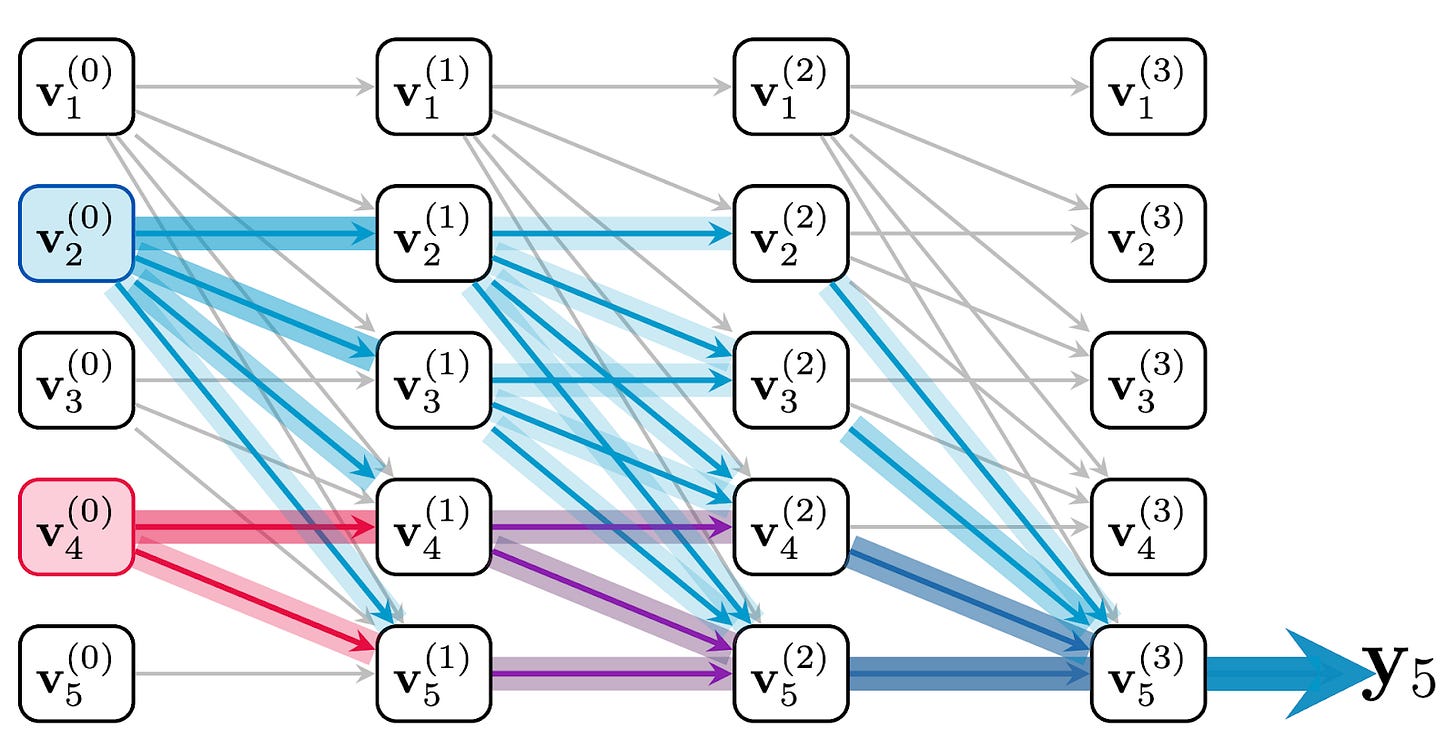
Why does this happen? At a high-level it’s because, as the sequence length increases, there are exponentially more paths for the information of earlier tokens in the sequence to propagate to the last tokens’s representation than there are for the last token’s information to propagate there. This phenomenon is called squashing and, when hardly any of the information from the last token makes it to the final layer, it’s said to have been “over-squashed.” The figure below shows how this happens: The red token has fewer paths to travel to the final token than the blue token does, which demonstrates that earlier tokens tend to squash later ones.
This phenomenon can be formalized mathematically by analyzing how sensitive the output of the last token’s representation is to changes in each of its input tokens. When we do this, there are three possible cases:
The output might be equally sensitive to changes in early and late tokens,
The output might be more sensitive to early tokens and less sensitive to later tokens, or
The output might be less sensitive to early tokens and more sensitive to later tokens.
Based on the examples we’ve looked at, can you tell which of the above three cases the transformer exhibits? If you said the second case, you’re correct! That is, the output is more sensitive to changes in earlier tokens and less sensitive to changes in later tokens. (If you’re following along with the paper, this is stated in Theorem 5.1 and proved in Appendix Theorem B.5.)
The reason the transformer exhibits this behavior has to do with the number of paths between the input tokens and the output representation. This idea of studying paths between two points is related to a mathematical concept called curvature. You can think of the general concept as categorizing the local shape of a space as either spherical (nearby parallel lines converge), Euclidean (nearby parallel lines remain parallel), or hyperbolic (nearby parallel lines diverge). Intuitively, this concept gives you a sense of whether the space around a point is expanding or contracting. One specific kind of curvature called Gaussian curvature describes how curved a 2d manifold (a curved surface) is at a particular point — its value, shown in parentheses below, indicates the shape at the points shown by the black dots.
(Fun fact: Ricci curvature — another measure of the curvature of manifolds — also appears in Einstein’s field equations, where it corresponds to the curvature of spacetime due to energy and momentum! I’m not going to pretend like I understand these equations, but if you’d like to learn more you can read about the connection between neural networks and spacetime in this awesome blog post.)
When we talk about graphs — like the the paths in the transformer — we’re talking about another specific kind of curvature called the balanced Forman curvature (as defined in this paper). This concept is another way you could mathematically capture the behavior of information flow that biases the last token toward receiving more data from earlier tokens and less from later tokens. In fact, the over-squashing phenomenon was first observed in another kind of neural network architecture called graph neural networks where over-squashing can occur between edges in a graph that have a small number of paths between them, like in the tree depicted below.
Theory aside, what are the consequences of this analysis? A practical consequence is that a sequence can get so long to the point that it’s literally impossible for later tokens’ information to propagate to the last token’s output, since the information has been over-squashed to the point that the precision of floating-point numbers can’t capture it anymore. It also means that — and this is my favorite takeaway from the paper — transformers are really bad at counting. As a transformer counts more numbers, it will eventually forget what the most recently counted numbers were, and they’ll essentially all blur together to the point that it doesn’t know what number should come next! 😂
While this is fascinating, the above discussion is a bit of a simplification of reality since it ignores attention weights. These weights also influence the curvature of information propagation and whether over-squashing will occur. In practice, transformers might learn to pay more attention to the tokens that appear later in the sequence.
The researchers also point to a simple way to reduce over-squashing: insert additional tokens, like a comma every three digits in the ones-and-zero example I described. This strategy helps to keep the representations more distant. More permanent solutions might involve modifying the transformer’s architecture, like how this paper adds more edges to the GNN where the Ricci curvature is the most negative. In practice, you probably don’t need to understand differential geometry (I certainly don’t!) in order to use transformers for something practical, but this paper is a helpful reminder that sometimes things aren’t as simple as our brains might pretend they are.